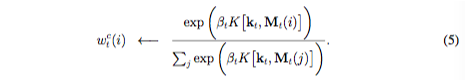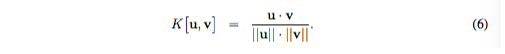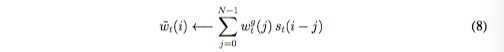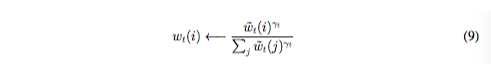近期,Google Deep Mind团队提出了一个机器学习模型,并起了一个特别高大上的名字:神经网络图灵机,我为大家翻译了这篇文章,翻译得不是特别好,有些语句没读明白,欢迎大家批评指正 🙂
原论文出处:http://arxiv.org/pdf/1410.5401v1.pdf。
版权所有,禁止转载。
神经网络图灵机
Alex Graves gravesa@google.com
Greg Wayne gregwayne@google.com
Ivo Danihelka danihelka@google.com
Google DeepMind, London, UK
摘要
本文通过引入一个使用注意力程序进行交互的外部存储器(external memory)来增强神经网络的能力。新系统可以与图灵机或者冯·诺依曼体系相类比,但每个组成部分都是可微的,可以使用梯度下降进行高效训练。初步的结果显示神经网络图灵机能够从输入和输出样本中推理出(infer)简单的算法,如复制、排序和回忆。
1. 简介
计算机程序在执行计算任务的过程中(Von Neumann, 1945)使用了三个基本机制:初等运算(如算术操作),逻辑控制流(分支循环)和可读写的存储器。虽然在建模复杂数据方面取得了广泛的成功,现代机器学习理论却普遍忽略了对控制流和存储器的使用。
由于其对带有时间属性的数据的进行学习和复杂转换的能力,递归神经网络脱颖而出。进一步,RNN又被证明是图灵完全等价的 (Siegelmann and Sontag, 1995),因而只要合理建模,它就可以模拟任何计算过程。但是理论上可行不代表实践中容易实现。为此,我们增强了标准递归网络的能力从而使算法型机器学习任务的解决方案得到简化。这个增强方案主要是依赖一个较大的、可寻址的存储器,而相似地,图灵机使用一个无穷存储带增强了有穷状态机,因而,我们称这种新设备为”神经网络图灵机”。不同于图灵机的是,NTM是一个可微的计算机,能够使用梯度下降进行训练,对于学习程序来说是一个很实用的机制。
在人类认知能力中, the process that shares the most similarity to algorithmic operation is known as “working memory.”。在神经生理学中,工作记忆的运行机制尚不清楚,根据字面意思,可以理解为是信息的短期存储和基于规则的操作集合(Baddeley et al., 2009)。在计算机术语中,这些规则就是程序,存储的信息构成了这些程序的参数。既然NTM被设计用来对“快速创建的变量”应用近似的规则,所以它模仿了一个工作记忆系统。快速创建的变量(Rapidly-created variables) (Hadley, 2009) 是可以快速绑定到存储槽的数据,就像传统计算机中数字3和4被放在寄存器然后相加得到7(Minsky, 1967)。由于NTM架构使用了注意过程来对存储器进行选择性读写,所以NTM使用了另一个相似的工作记忆模型。与大多数工作记忆模型相比,我们的架构能够学习使用他的工作记忆,而不需要为符号数据引入一系列固定的程序。
本文首先对在心理学、语言学和神经科学以及人工智能和神经网络等领域与工作记忆相关的研究做一简单回顾。然后描述我们的主要工作,一个存储架构和注意力控制器,并且我们相信这个控制器可以满足简单程序的归纳(induction)和执行(execution)这类任务的性能要求。为了测试这个结构,我们设计了一些问题,并给出了详细的测试结果。最后总结这个架构的有点。
2. 基础研究
2.1 心理学和神经科学
工作记忆的概念在心理学中得到比较深入的研究,并用来解释短期信息处理时的性能问题。其大致的构成是一个”中央执行器“聚焦注意力和对记忆缓存中的数据进行各种操作(Baddeley等, 2009)。心理学家已经充分研究了工作记忆的容量限制,通常使用信息组块的数量来衡量,这种信息组块可以被轻松地回忆起来(Miller,1956)。因为容量限制的存在,使得我们能够理解人类大脑记忆系统中的结构性约束。
神经科学中,工作记忆过程被认为是前额叶皮层和基底神经节整合系统的功能(Goldman-Rakic, 1995)。
典型的实验如,让猴子观察一个短暂的提示,然后经过一个延迟时间,再根据这个提示以一种方式进行响应,同时,观察其前额叶皮层的一个或一组神经元的状态。特定的任务可以使神经元在延迟期间持续激活或者呈现更复杂的神经动力学特征。最近的一个研究量化了在执行某个任务的延迟期间的额叶皮层活动,这是一个基于众码(population code)维度来度量的复杂且上下文无关的任务,可以用来预测记忆的性能(Rigotti et al., 2013)。
还有一些工作记忆的建模研究,有的在研究生物回路是如何实现持续神经元激活的(Wang, 1999),有的研究如何实现具体的任务(Hazy等,2006)(Dayan, 2008)(Eliasmith, 2013)。当然Hazy等人的模型我们的工作比较相关,因为它也类似于LSTM架构,我们也是基于其进行的改造。像我们的架构一样,Hazy等人设计了一些机制将信息放入到内存槽中,这个内存槽,被用来处理基于内部规则构建的内存任务。与我们的工作相对比,这些作者并没有引入内存寻址的先进理念,从而限制了这些系统只能进行简单数据的存储和回忆。尽管Gallistel和King (Gallistel and King, 2009)和Marcus (Marcus, 2003) 强调大脑的操作一定包含寻址,却经常被神经科学的计算模型所遗忘,而这正是我们工作的基础。
2.2 认知科学和语言学
历史上,认知科学和语言学与人工智能学科几乎是同时出现的,他们都深深地受到计算机的影响(Chomsky, 1956) (Miller, 2003)。他们的目的都是基于信息或符号处理机制解释人的精神活动。早在20世纪80年代,这两个领域就都认为递归式和过程式(基于规则的)符号处理是认知的最高级形式(highest mark)。The Parallel Distributed Processing (PDP) or connectionist revolution cast aside the symbol-processing metaphor in favour of a so-called “sub-symbolic” description of thought processes (Rumelhart et al., 1986).
Fodor和Pylyshyn (Fodor and Pylyshyn, 1988) 发表了两个关于认知模型神经网络的局限性的重要证明。他们首先指出联结理论不能解决变量绑定(variable-binding)问题,即不能对数据结构中特定槽位(slot)赋值特定的数据。语言中,变量绑定无处不在,例如,当人对“Mary spoke to John”这种形式的句子进行理解的时候,首先会将Mary赋值为主语,John赋值为宾语,而“spoke to”则赋值为谓语。Fodor和Pylyshyn也讨论到带有定长输入域的神经网络无法产生像人类这样的变长结构处理能力。针对这个论断,包括Hinton (Hinton, 1986), Smolensky (Smolensky, 1990), Touretzky (Touretzky, 1990), Pollack (Pollack, 1990), Plate (Plate, 2003), and Kanerva (Kanerva, 2009)在内的神经网络研究者们研究了特定的机制以在联接框架内支持变量绑定和变量结构。我们的架构借鉴并增强了这项工作。
变长结构的递归处理是人类认知的重要特点。在过去的十年中,a firefight in the linguistics community staked several leaders of the field against one another。目前的问题是递归处理是否是“独特人类”产生语言的进化创新,为语言所独有,Fitch, Hauser, and Chomsky (Fitch等, 2005)支持这种观点,还是多种其他的变化来负责人类语言的进化,而递归处理早于语言出现(Jackendoff and Pinker, 2005)。当然无论递归处理的进化源头是什么,所有人都同意它是人类认知灵活度的核心要素。
2.3 递归神经网络
递归神经网络(RNN)是一类带有动态状态的机器;它的状态可以根据当前的内部状态和输入进行迁移。对比也包含动态状态的隐式马尔可夫链,RNN的状态是分布式的,因而有更大的存储能力和计算能力。动态状态十分重要,因为它使得基于上下文的计算称为可能;在某一时刻的信号能够改变后面时刻的网络行为。
递归网络的一个重要创新是LSTM(Hochreiter and Schmidhuber, 1997),是一种为解决“vanishing and exploding gradient”问题而开发的一个通用架构。它在网络中嵌入了一些完美的集成器用作内部存储 (Seung, 1998) 。集成器最简单的一个例子是x(t + 1) = x(t) + i(t),i(t)是系统的输入。内部表示矩阵Ix(t)意味着信号不会动态地消失或爆炸。如果给集成器配置一个基于上下文的内部网络(称为门gate电路),得到等式x(t + 1) = x(t) + g(context)i(t),我们就可以在无限长的时间内选择性地存储信息。
递归网络不需要任何修改就可以很容易地处理变长结构(variable-length structures)。在序列问题中,网络的输入在不同时间到达,允许跨多个时间步处理变长或组合结构。由于递归网络可以本地(natively)处理变长结构,所以最近被应用于语音识别(Graves等, 2013; Graves and Jaitly, 2014),文本生成(Sutskever等, 2011),手写字生成 (Graves, 2013) 和机器翻译 (Sutskever et al., 2014)等各种认知问题。考虑到这个特性,我们认为通过显示地建立分析树来聚合组合结构(Pollack, 1990) (Socher等, 2012) (Frasconi等, 1998)并不是最迫切或者有价值的。我们的工作的一些其他重要前提还包括通过递归网络构建的注意力可微模型(Graves, 2013) (Bahdanau等, 2014)和程序搜索(Hochreiter等, 2001b)(Das等, 1992)。
3. 神经网络图灵机
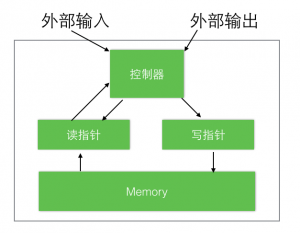
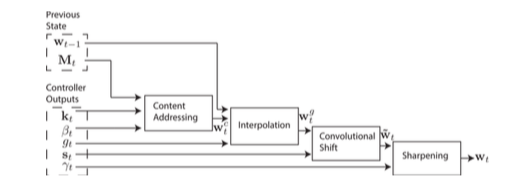
图1
神经网络图灵机(NTM)架构包含两个基本组件:神经网络控制器和内存池。图1展示了NTM的一个高层面流程图。像大多数神经网络一样,控制器通过输入输出向量与外界交互,但不同于标准网络的是,它还与一个带有选择性读写操作的内存矩阵进行交互。类比图灵机,我们将执行读写操作的网络输出称为“头”heads(译者注:后面有时会翻译成指针)。
特别重要地,架构中的每个组件都是可微分的,这使得梯度下降训练更为直接,为此,我们定义了“模糊”读写的概念,即可以通过不同的权重与内存中的全部元素进行交互(与此相应的则是图灵机和数字计算机中的单一元素寻址操作)。通过限制读写操作的值针对内存中的一小部分进行操作的同时忽略其他部分,我们引入了一种可以确定“模糊度”的“注意力聚焦”机制。由于与内存的交互高度离散,NTM网络更擅长存储数据而很少收到干扰。读写头上的特定输出决定了代表注意力焦点的内存地址。这些输出其实就是一个代表在内存矩阵上的各行归一化权重的表示(称为内存“地址集合”)。每个读写头都有一个权重列表,这个权重列表代表了它的读写头在各个地址的读写比重(degree),也就是说,一个读写头,既可以全部精力访问一个单一地址,也可以分散精力在不同的地址上。(译者注:这个精力就是总比重,weighting就是定义了整个内存空间,每个位置的读写比重,至于读写比重的意义,在后面就可以体会到)。
3.1 读
令M_t代表时刻t的N×M内存矩阵。(N代表地址数或行数,M代表每个地址的向量大小)。令W_t在时刻t读写头在N个地址的读写比重,由于所有的权重都进行了归一化,所以W_t向量的内部元素W_t(i)满足:
那么,时刻t读取到的值R_t,可以定义为每个地址的向量Mt(i)加权和:sum
这个公式清晰地将内存和权重分离了出来。
3.2 写
受LSTM中的forget gate和输入的启发,我们将写操作拆分成两个部分:先擦除(erase)在添加(add)。
给定t时刻的写头权重w_t,以及一个擦出向量e_t,其中M个元素均在0~1范围内,则t-1时刻的内存向量在t时刻将按下式进行调整:
其中1是一个全部是1的行向量。当e_t为全零向量时,整个内存就会被重置为零。若权重为零或者擦除向量为零,则内存保持不变。当多个写头同时存在时,多个操作可以以任意顺序相互叠加。
而加向量a_t,是在擦除动作之后执行下面动作:
同样,多个写头的添加动作的先后顺序也是无关的,经过这些擦除动作和添加动作之后,可以得到t时刻的最终内存结果。既然擦除和添加两种动作是可微的,组合写的动作也是各自独立微分的。注意,擦除和添加动作都有M个独立部分,使得对每个内存地址的修改可以在更细的粒度上进行。
3.3 寻址机制
前面我们给出了读写的公式,但我们没有说明权重是如何产生的。权重是通过两种寻址机制以及一些其他补充机制的共同作用产生的。第一种机制,“基于内容的寻址”,基于依据控制器提供的值与当前值的相似度来决定对内存地址的聚焦程度。这个机制与Hopfield网络(Hopfield, 1982)的地址寻址是相关的。地址寻址的优点是提取非常简单,仅仅需要控制器产生一个与存储数据的一部分相似的数据即可,这个数据被用来与内存比较,然后获取到精确的存储值。
但并不是所有的问题都适合内存寻址。在特定任务中,变量的内容就非常随机的,但变量仍然需要一个可识别的名字或者地址。算术问题就属于这一类:变量x和变量y可以代表任意两个值,而 f (x, y) = x × y是一个明确的定义的程序过程。针对这种任务的控制处接收变量x和y的值,将他们存储在不同的地址中,然后获取他们再执行乘法操作 。这个例子中,变量是通过指定地址寻址的,而不是内容。我们称之为“指定地址寻址”。内容寻址比地址寻址严格来说更为通用,因为内容寻址本身可能包含地址信息。但在我们的实验证明提供地址寻址功能,对某些形式的通用化很有必要,所以我们同时引入了两种寻址机制。
图2是整个寻址系统的流程图,展示了在读写时,生成权重向量的操作序列。
图2. 寻址机制的流程图。向量key,k_t,和key的强度β_t,用作内容寻址。内容寻址的权重被key作用后会基于上一时刻的权重和gate值g_t进行插值调整。 随后位移向量s_t会决定是否或者进行多少的旋转操作。最后,依赖于γ_t, 权重会被sharpen以用于内存访问。
3.3.1 按内容聚焦
对于内容寻址,每个读写头都首先产生一个M长度的key向量k_t,并通过一个相似度度量函数K[.,.]分别与每个行向量M_t(i)逐一比较。基于内容的系统会基于相似度和key的强度产生一个归一化的权重列表w_{t}^{c},β_t可以放大或减弱聚焦的精度。
在我们当前的实现中,相似度度量函数用的是余弦相似:
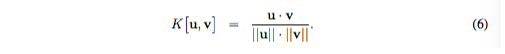
3.3.2 按地址聚焦
基于指定地址的寻址机制既可以用做简单的内存空间遍历,也可以用于随机访问。这是通过对weighting的一个旋转位移操作来实现的。举例,如果当前权重定义为全力聚焦在一个单一地址上,那么一个为1的旋转可以位移到下一个地址,一个负的位移则相反。
先于旋转操作,每个读写头还具有一个标量代表插值门g_t,取值0~1,g值被用作混合前一时刻中读写头产生的w_{t-1}和当前时刻中有内容系统产生的权重列表w_{t}^{c},进而推导出门控制后(gated)权重列表w_{t}^{g}:
如果gate是0,那么整个内容权重就被完全忽略,而来自前一个时刻的权重列表就被直接使用。相反,如果gate值是1,那么就完全采用内容寻址的结果。
在插值(interpolation)之后,每个读写头都会给出一个位移权重S_t,用于定义一个在允许的整数值位移上的归一化分布。例如,如果-1和1被用作位移,则s_t有三个元素分别代表-1,0,1执行后的位移程度。The simplest way to define the shift weightings is to use a softmax layer of the appropriate size attached to the controller。我们也尝试了另一个方法,让控制器给出一个单一标量,用来表示一个在前一种统一分布的下界。例如,如果位移标量为6.7,那么s_t(6) = 0.3,s_t(7) = 0.7,剩下的s_t(i)均为0。
如果内存地址为0到N-1,使用s_t来旋转w_{t}^{g},可以使用下面的循环卷积来表示:
其中,all index arithmetic is computed modulo N,如果位移权重不是sharp的,那么公式8中的卷积操作能够导致权重随时间发散。例如,如果给-1,0,1的对应的权重0.1,0.8和0.1,则旋转就会将一个聚焦在一个点上的权重变成轻微模糊在三个点上。为了解决这个问题,每个读写头最后会给出一个标量γ_t ≥ 1用来sharpen最终的权重:
结合权重插值、内容寻址和地址寻址的寻址系统可以在三种补充(complementary)模式下工作。第一,权重列表可以由内容系统来自主选择而不被地址系统所修改。第二,有内容系统产生的权重可以再选择和位移。这使得焦点能够跳跃到通过内容寻址产生的地址附近而不是只能在其上。在计算方面,这使得读写头可以访问一个连续的数据块,并访问这个块中特定数据。第三,来自上一个时刻的权重可以在没有任何内容系统输入的情况下被旋转,以便权重可以以相同的时间间隔连续地访问一个地址序列。
3.4 控制网络
上面描述的NTM架构有三个自由参数,内存的大小,读写头的数量,允许的地址位移范围。但或许最重要的架构选择是用作控制器的网络模型。尤其是,我们可以决定使用前馈网络(FN)还是递归网络(RN)。诸如LSTM这样的递归控制器拥有自己的内部存储器,这个存储器可以对矩阵中更大的存储器起到补充作用。如果将控制器比作数字计算机的中央处理器单元(albeit with adaptive rather than predefined instructions) ,将内存矩阵比作RAM,那么递归网络的隐藏激活神经元们(hidden activations)就像是处理器的寄存器。他们允许控制器跨时间操作时能够共享信息。另一方面,一个前馈网络控制器可以通过每一时刻都读写同一地址来模拟递归网络。进一步,前馈控制器通常给予网络操作更大的透明度,因为对内存矩阵的读写模式通常比RNN的内部状态更容易解释。然而,前馈网络的一个局限性是并行读写头的数量,在执行计算任务时会成为瓶颈。一个单一读出头在每个时刻只能对每个内存向量执行一元变换,而两个读出头就可以二元向量变换,以此类推。递归控制器则能够存储上一时刻的读出的向量,不会受到这个限制。
4. 实验
4.1 复制
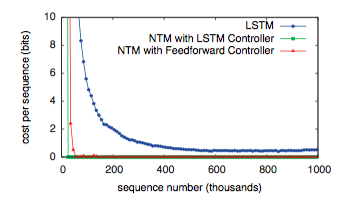
复制任务用来测试NTM能否存储并回忆起一个任意信息的长序列。首先想网络输入一个任意二进制向量组成的序列,并跟随一个分隔符。跨域长时间周期对信息进行存储和访问对RNN和其他动态架构来说一个难题。我们很想知道NTM比LSTM是否能胜任更长的时间。
图3. Copy Learning Curves.
网络使用任意8字节向量组成的序列来训练,序列的长度在1到20之间随机。目标序列是输入的副本,只是不带分隔符。注意,在接受(从哪里接受?)目标序列时不对网络进行任何输入,这样确保在网络回忆整个序列时没有借助任何中间过程。如图3所示,NTM(无论使用前馈还是LSTM的控制器)比LSTM本身都学习的更快,消耗更小。NTM和LSTM学习曲线的差距足以说明这已经是质的不同,而不仅仅是量的不同。
图4. NTM Generalisation on the Copy Task. The four pairs of plots in the top row depict network outputs and corresponding copy targets for test sequences of length 10, 20, 30, and 50, respectively. The plots in the bottom row are for a length 120 sequence. The network was only trained on sequences of up to length 20. The first four sequences are reproduced with high confidence and very few mistakes. The longest one has a few more local errors and one global error: at the point indicated by the red arrow at the bottom, a single vector is duplicated, pushing all subsequent vectors one step back. Despite being subjectively close to a correct copy, this leads to a high loss.
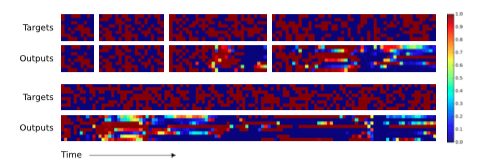
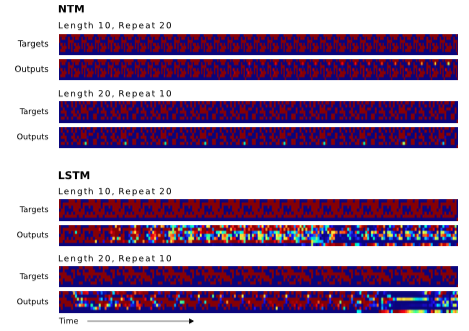
图5. LSTM Generalisation on the Copy Task. The plots show inputs and outputs for the same sequence lengths as Figure 4. Like NTM, LSTM learns to reproduce sequences of up to length 20 almost perfectly. However it clearly fails to generalise to longer sequences. Also note that the length of the accurate prefix decreases as the sequence length increases, suggesting that the network has trouble retaining information for long periods.
我们研究了网络在训练过程不只是看到而是能否归纳更长的序列的能力(很显然他能否从训练错误中学习到在面对新的向量时要更加通用。)图4和图5说明这个过程中LSTM和NTM的行为是完全不同的。NTM能够随着长度的增加持续进行复制工作,而LSTM在超过20后迅速失效。
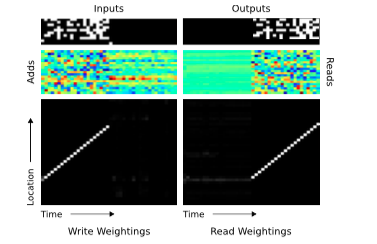
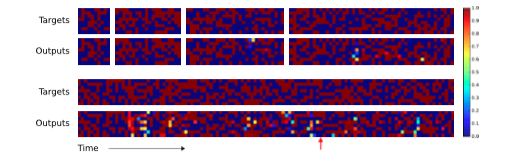
图6. NTM Memory Use During the Copy Task. The plots in the left column depict the inputs to the network (top), the vectors added to memory (middle) and the corresponding write weightings (bottom) during a single test sequence for the copy task. The plots on the right show the outputs from the network (top), the vectors read from memory (middle) and the read weightings (bottom). Only a subset of memory locations are shown. Notice the sharp focus of all the weightings on a single location in memory (black is weight zero, white is weight one). Also note the translation of the focal point over time, reflects the network’s use of iterative shifts for location-based addressing, as described in Section 3.3.2. Lastly, observe that the read locations exactly match the write locations, and the read vectors match the add vectors. This suggests that the network writes each input vector in turn to a specific memory location during the input phase, then reads from the same location sequence during the output phase.
后续的分析表明,NTM不像LSTM能够学习到复制算法的某种形式。为了确定这是一种什么算法,我们查看了控制器与内存之间的交互信息(图6),最后确认网络所进行的操作序列可以总结成一下伪代码:
initialise: move head to start location
while input delimiter not seen do
receive input vector
write input to head location increment head location by 1
end while
return head to start location
while true do
read output vector from head location
emit output
increment head location by 1
end while
这实际就是人类程序员在执行相同任务时的低级语言代码。从数据结构方面来说,NTM已经学会了如何创建和迭代数组。注意,该算法结合了内容寻址(跳到开始位置)和地址寻址(沿着序列移动)。还要注意到如果没有基于前一个时刻的读写权重进行位移(公式7)的能力的话,迭代也无法具有处理更长序列的能力,另外如果如果没有焦点锐化(focus-sharpening)能力(公式9)的话,权重就是随着时间的推移开始失真。
4.2 循环复制
循环复制任务时复制任务的一个扩展,它要求网络能够输出复制的序列一个指定的次数,并在最后打一个标记。这个主要用来查看NTM能否学会简单的嵌套函数。理想情况下,我们希望它能循环执行一个它学习过的子程序。
网络接收一个随机长度的序列,之后在一个独立的输入通道输入一个标量值代表希望复制的次数。为了在恰当的时间输出结束标记,网络不但要能够理解外部输入,还要记住已经执行了几次。和复制任务一样,在初始化序列和循环次数输入给网络之后,不再进行任何输入。训练网络重现随机二进制8位向量序列,其中序列长度和重复次数都从1-10中随机选取。代表重复次数的输入被标准化,期望为0,方差为1.
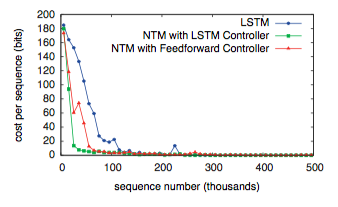
图7. Repeat Copy Learning Curves.
图7显示NTM学习这个任务比LSTM快得多,但两者都能很好的执行这个任务。在被问及针对训练数据的泛化时,两个架构的不同才变得清晰。这个案例中,我们对两个维度的泛化感兴趣:序列长度和重复次数。图8说明了两次复制的效果,其中LSTM两个测试都失败了,儿NTM在更长的序列上都成功了,并且能否成功执行超过十次;但是它不能记录他已经完成了多少次,所以无法正确地输出结束标记。这也许是因为使用小数表示循环次数的原因,因为在固定的范围它很难被泛化。
图8. NTM and LSTM Generalisation for the Repeat Copy Task. NTM generalises almost perfectly to longer sequences than seen during training. When the number of repeats is increased it is able to continue duplicating the input sequence fairly accurately; but it is unable to predict when the sequence will end, emitting the end marker after the end of every repetition beyond the eleventh. LSTM struggles with both increased length and number, rapidly diverging from the input sequence in both cases.
图8说明NTM学习了一种复制算法的扩展算法,能够尽量多地重复读取。
4.3 4.4 4.5 4.6
【翻译中】
5. 结语
受生物学中工作记忆和数字计算机的设计启发,我们发明了神经网络图灵机。跟传统神经网络一样,该架构是端到端可微的,可以被梯度下降算法训练。我们的实验证明,这个架构可以从样本数据中学会简单的算法,并可以很好地在训练样本之外应用这个学到的算法。
6 Acknowledgments
Many have offered thoughtful insights, but we would especially like to thank Daan Wier- stra, Peter Dayan, Ilya Sutskever, Charles Blundell, Joel Veness, Koray Kavukcuoglu, Dharshan Kumaran, Georg Ostrovski, Chris Summerfield, Jeff Dean, Geoffrey Hinton, and Demis Hassabis.
References
- Baddeley, A., Eysenck, M., and Anderson, M. (2009). Memory. Psychology Press. Bahdanau, D., Cho, K., and Bengio, Y. (2014). Neural machine translation by jointly
- learning to align and translate. abs/1409.0473.
- Barrouillet, P., Bernardin, S., and Camos, V. (2004). Time constraints and resource shar- ing in adults’ working memory spans. Journal of Experimental Psychology: General, 133(1):83.
- Chomsky, N. (1956). Three models for the description of language. Information Theory, IEEE Transactions on, 2(3):113–124.
- Das, S., Giles, C. L., and Sun, G.-Z. (1992). Learning context-free grammars: Capabil- ities and limitations of a recurrent neural network with an external stack memory. In Proceedings of The Fourteenth Annual Conference of Cognitive Science Society. Indiana University.
- Dayan, P. (2008). Simple substrates for complex cognition. Frontiers in neuroscience, 2(2):255.
- Eliasmith, C. (2013). How to build a brain: A neural architecture for biological cognition. Oxford University Press.
- Fitch, W., Hauser, M. D., and Chomsky, N. (2005). The evolution of the language faculty: clarifications and implications. Cognition, 97(2):179–210.
- Fodor, J. A. and Pylyshyn, Z. W. (1988). Connectionism and cognitive architecture: A critical analysis. Cognition, 28(1):3–71.
- Frasconi, P., Gori, M., and Sperduti, A. (1998). A general framework for adaptive process- ing of data structures. Neural Networks, IEEE Transactions on, 9(5):768–786.
- Gallistel, C. R. and King, A. P. (2009). Memory and the computational brain: Why cogni- tive science will transform neuroscience, volume 3. John Wiley & Sons.
- Goldman-Rakic, P. S. (1995). Cellular basis of working memory. Neuron, 14(3):477–485. Graves, A. (2013). Generating sequences with recurrent neural networks. arXiv preprint
- arXiv:1308.0850.
- Graves, A. and Jaitly, N. (2014). Towards end-to-end speech recognition with recurrent neural networks. In Proceedings of the 31st International Conference on Machine Learn- ing (ICML-14), pages 1764–1772.
- Graves, A., Mohamed, A., and Hinton, G. (2013). Speech recognition with deep recurrent neural networks. In Acoustics, Speech and Signal Processing (ICASSP), 2013 IEEE International Conference on, pages 6645–6649. IEEE.
- Hadley, R. F. (2009). The problem of rapid variable creation. Neural computation, 21(2):510–532.
- Hazy, T. E., Frank, M. J., and O’Reilly, R. C. (2006). Banishing the homunculus: making working memory work. Neuroscience, 139(1):105–118.
- Hinton, G. E. (1986). Learning distributed representations of concepts. In Proceedings of the eighth annual conference of the cognitive science society, volume 1, page 12. Amherst, MA.
- Hochreiter, S., Bengio, Y., Frasconi, P., and Schmidhuber, J. (2001a). Gradient flow in recurrent nets: the difficulty of learning long-term dependencies.
- Hochreiter, S. and Schmidhuber, J. (1997). Long short-term memory. Neural computation, 9(8):1735–1780.
- Hochreiter, S., Younger, A. S., and Conwell, P. R. (2001b). Learning to learn using gradient descent. In Artificial Neural Networks?ICANN 2001, pages 87–94. Springer.
- Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the national academy of sciences, 79(8):2554– 2558.
- Jackendoff, R. and Pinker, S. (2005). The nature of the language faculty and its implications for evolution of language (reply to fitch, hauser, and chomsky). Cognition, 97(2):211– 225.
- Kanerva, P. (2009). Hyperdimensional computing: An introduction to computing in dis- tributed representation with high-dimensional random vectors. Cognitive Computation, 1(2):139–159.
- Marcus, G. F. (2003). The algebraic mind: Integrating connectionism and cognitive sci- ence. MIT press.
- Miller, G. A. (1956). The magical number seven, plus or minus two: some limits on our capacity for processing information. Psychological review, 63(2):81.
- Miller, G. A. (2003). The cognitive revolution: a historical perspective. Trends in cognitive sciences, 7(3):141–144.
- Minsky, M. L. (1967). Computation: finite and infinite machines. Prentice-Hall, Inc. Murphy, K. P. (2012). Machine learning: a probabilistic perspective. MIT press.
- Plate, T. A. (2003). Holographic Reduced Representation: Distributed representation for cognitive structures. CSLI.
- Pollack, J. B. (1990). Recursive distributed representations. Artificial Intelligence, 46(1):77–105.
- Rigotti, M., Barak, O., Warden, M. R., Wang, X.-J., Daw, N. D., Miller, E. K., and Fusi, S. (2013). The importance of mixed selectivity in complex cognitive tasks. Nature, 497(7451):585–590.
- Rumelhart, D. E., McClelland, J. L., Group, P. R., et al. (1986). Parallel distributed pro- cessing, volume 1. MIT press.
- Seung, H. S. (1998). Continuous attractors and oculomotor control. Neural Networks, 11(7):1253–1258.
- Siegelmann, H. T. and Sontag, E. D. (1995). On the computational power of neural nets. Journal of computer and system sciences, 50(1):132–150.
- Smolensky, P. (1990). Tensor product variable binding and the representation of symbolic structures in connectionist systems. Artificial intelligence, 46(1):159–216.
- Socher, R., Huval, B., Manning, C. D., and Ng, A. Y. (2012). Semantic compositionality through recursive matrix-vector spaces. In Proceedings of the 2012 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Lan- guage Learning, pages 1201–1211. Association for Computational Linguistics.
- Sutskever, I., Martens, J., and Hinton, G. E. (2011). Generating text with recurrent neural networks. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), pages 1017–1024.
- Sutskever, I., Vinyals, O., and Le, Q. V. (2014). Sequence to sequence learning with neural networks. arXiv preprint arXiv:1409.3215.
- Touretzky, D. S. (1990). Boltzcons: Dynamic symbol structures in a connectionist network. Artificial Intelligence, 46(1):5–46.
- Von Neumann, J. (1945). First draft of a report on the edvac.
- Wang, X.-J. (1999). Synaptic basis of cortical persistent activity: the importance of nmda
- receptors to working memory. The Journal of Neuroscience, 19(21):9587–9603.